Wybór odpowiedniego testu statystycznego jest kluczowy dla przeprowadzenia rzetelnej analizy danych. Rodzaj danych, które posiadamy, oraz cel analizy mają ogromne znaczenie dla podejmowania decyzji dotyczących testów, które należy zastosować. W tym artykule przedstawimy, jak różne typy danych — ilościowe i jakościowe — wpływają na wybór testów statystycznych, a także jakie założenia muszą być spełnione, aby wyniki były wiarygodne.
Warto zwrócić uwagę na to, że nie wszystkie testy są sobie równe. W zależności od tego, czy analizujemy dane ciągłe, czy kategoryczne, będziemy musieli zastosować różne podejścia. Dzięki tej wiedzy unikniemy błędów w analizie i uzyskamy bardziej precyzyjne wyniki.
Kluczowe informacje:- Rozróżnienie między danymi ilościowymi (np. wzrost, waga) a jakościowymi (np. płeć, kolor) jest fundamentalne dla wyboru testu.
- Dla danych ilościowych, jeśli spełnione są założenia normalności, stosuje się testy parametryczne, takie jak t-test czy ANOVA.
- Dla danych jakościowych kluczowym narzędziem jest test chi-kwadrat, który pozwala na analizę zależności między zmiennymi.
- Sprawdzanie założeń, takich jak normalność rozkładu i jednorodność wariancji, jest niezbędne przed zastosowaniem odpowiednich testów.
- W przypadku niespełnienia założeń, warto rozważyć testy nieparametryczne, które są bardziej uniwersalne.
Wybór testu statystycznego w zależności od rodzaju danych
Wybór odpowiedniego testu statystycznego jest kluczowy dla uzyskania wiarygodnych wyników analizy danych. Rodzaj danych, które posiadamy, ma istotny wpływ na to, jakie testy możemy zastosować. Możemy wyróżnić dwa główne typy danych: dane ilościowe i dane jakościowe. Każdy z tych typów wymaga innego podejścia do analizy, co wpłynie na dobór testu statystycznego.
Dane ilościowe to wartości liczbowe, które można mierzyć i porównywać. Przykładami danych ilościowych są wzrost, waga czy wyniki testów. Z kolei dane jakościowe to kategorie, które opisują cechy, takie jak płeć, kolor oczu czy typ wykształcenia. W przypadku danych ilościowych można stosować testy takie jak t-test czy analiza wariancji (ANOVA), natomiast dla danych jakościowych najczęściej używa się testu chi-kwadrat.
Jakie są różnice między danymi ilościowymi a jakościowymi?
Dane ilościowe i jakościowe różnią się przede wszystkim sposobem, w jaki są zbierane i analizowane. Dane ilościowe są mierzone w jednostkach liczbowych i można je poddać różnym operacjom matematycznym. Na przykład, średnia waga grupy osób jest wartością, którą można obliczyć. Dane jakościowe z kolei są klasyfikowane w kategorie, które nie mają wartości liczbowych. Przykładem może być klasyfikacja osób według ich ulubionego koloru, gdzie nie możemy zastosować operacji matematycznych.
Jakie testy statystyczne stosować dla danych ilościowych?
Dla danych ilościowych istnieje wiele testów statystycznych, które mogą być zastosowane w zależności od celu analizy. Test t-Studenta jest często używany do porównania średnich dwóch grup, na przykład, aby sprawdzić, czy średnia waga mężczyzn różni się od średniej waga kobiet. W przypadku porównania więcej niż dwóch grup, stosuje się analizę wariancji (ANOVA), która pozwala na jednoczesne porównanie średnich w kilku grupach. Ważne jest, aby przed zastosowaniem tych testów upewnić się, że dane spełniają odpowiednie założenia, takie jak normalność rozkładu.
| Typ danych | Test statystyczny | Przykłady zastosowania |
| Ilościowe | t-test | Porównanie średnich dwóch grup |
| Ilościowe | ANOVA | Porównanie średnich w więcej niż dwóch grupach |
| Jakościowe | Chi-kwadrat | Analiza zależności między zmiennymi jakościowymi |
Jakie testy statystyczne stosować dla danych jakościowych?
Dla danych jakościowych kluczowym narzędziem analitycznym jest test chi-kwadrat. Ten test pozwala na ocenę, czy istnieje związek między dwiema zmiennymi jakościowymi. Na przykład, można go zastosować do analizy, czy płeć (mężczyzna/kobieta) wpływa na preferencje dotyczące rodzaju napoju (kawa/herbata). Test chi-kwadrat może być użyty zarówno w przypadku danych z jedną zmienną jakościową, gdzie stosuje się test chi-kwadrat jednozmiennowy, jak i w przypadku dwóch zmiennych jakościowych, gdzie używa się testu chi-kwadrat dwuzmiennowego.
Warto również zauważyć, że test chi-kwadrat wymaga spełnienia pewnych założeń, takich jak odpowiednia liczba obserwacji w każdej kategorii. W przypadku, gdy liczba obserwacji jest zbyt mała, można rozważyć zastosowanie alternatywnych testów, takich jak test Fishera, który jest bardziej odpowiedni dla małych próbek. Test chi-kwadrat jest szeroko stosowany w badaniach społecznych, marketingowych oraz w analizach zdrowotnych.
| Typ testu | Opis | Przykład zastosowania |
| Chi-kwadrat jednozmiennowy | Sprawdza, czy rozkład liczebności w grupach jest zbliżony | Analiza preferencji wyboru napoju w grupie osób |
| Chi-kwadrat dwuzmiennowy | Ocena związku między dwiema zmiennymi jakościowymi | Badanie zależności między płcią a preferencjami napojów |
Jak sprawdzić normalność rozkładu danych?
Aby ocenić normalność rozkładu danych, można zastosować zarówno metody wizualne, jak i statystyczne. Jednym z najpopularniejszych testów statystycznych jest test Shapiro-Wilka, który sprawdza, czy próbka danych pochodzi z rozkładu normalnego. Jeśli wartość p uzyskana z tego testu jest mniejsza niż ustalony poziom istotności (np. 0,05), można odrzucić hipotezę o normalności. Inną metodą wizualną jest wykres Q-Q (Quantile-Quantile), który porównuje kwantyle danych z kwantylami rozkładu normalnego. Jeśli punkty na wykresie układają się w linię prostą, sugeruje to normalność rozkładu.
Dlaczego jednorodność wariancji jest istotna w analizie?
Jednorodność wariancji to założenie, które mówi, że wariancje grup porównywanych w analizie statystycznej powinny być podobne. Jest to kluczowy warunek dla wielu testów statystycznych, takich jak ANOVA czy t-test. Jeśli wariancje są znacznie różne, może to prowadzić do nieprawidłowych wniosków i zwiększonego ryzyka błędów typu I lub II. Dlatego przed przystąpieniem do analizy danych, warto przeprowadzić testy, takie jak test Levene’a, aby sprawdzić, czy założenie jednorodności wariancji jest spełnione.
Jakie testy wybrać w badaniach porównawczych?
W badaniach porównawczych kluczowym narzędziem są testy statystyczne, które pozwalają na analizę różnic między grupami. Test t-Studenta jest najczęściej stosowany do porównania średnich dwóch grup, na przykład w badaniach dotyczących wpływu diety na wagę ciała, gdzie można porównać grupę stosującą dietę niskokaloryczną z grupą kontrolną. W przypadku, gdy chcemy porównać średnie w więcej niż dwóch grupach, odpowiednim narzędziem jest analiza wariancji (ANOVA), która umożliwia jednoczesne porównanie wielu grup, na przykład różnych metod leczenia w badaniach medycznych.
Warto również zauważyć, że przed zastosowaniem tych testów należy upewnić się, że spełnione są odpowiednie założenia, takie jak normalność rozkładu i jednorodność wariancji. Testy porównawcze są szeroko stosowane w różnych dziedzinach, od psychologii po biologię, i pozwalają na uzyskanie istotnych wniosków dotyczących badanych zjawisk.
Jakie testy stosować w analizie korelacji między zmiennymi?
W analizie korelacji między zmiennymi istotne są testy korelacji, które pozwalają na ocenę związku między dwiema zmiennymi ilościowymi. Najpopularniejszym z nich jest współczynnik korelacji Pearsona, który mierzy siłę i kierunek liniowej zależności między dwiema zmiennymi, na przykład między czasem nauki a wynikami w teście. W sytuacjach, gdy dane nie spełniają założeń normalności, można zastosować współczynnik korelacji Spearmana, który jest nieparametrycznym odpowiednikiem i ocenia monotoniczne zależności.
Testy korelacji są niezwykle przydatne w badaniach społecznych, ekonomicznych oraz zdrowotnych, ponieważ pozwalają na zrozumienie, jak różne czynniki wpływają na siebie nawzajem. Warto pamiętać, że korelacja nie oznacza przyczynowości; nawet silny związek może nie wskazywać na to, że jedna zmienna wpływa na drugą.
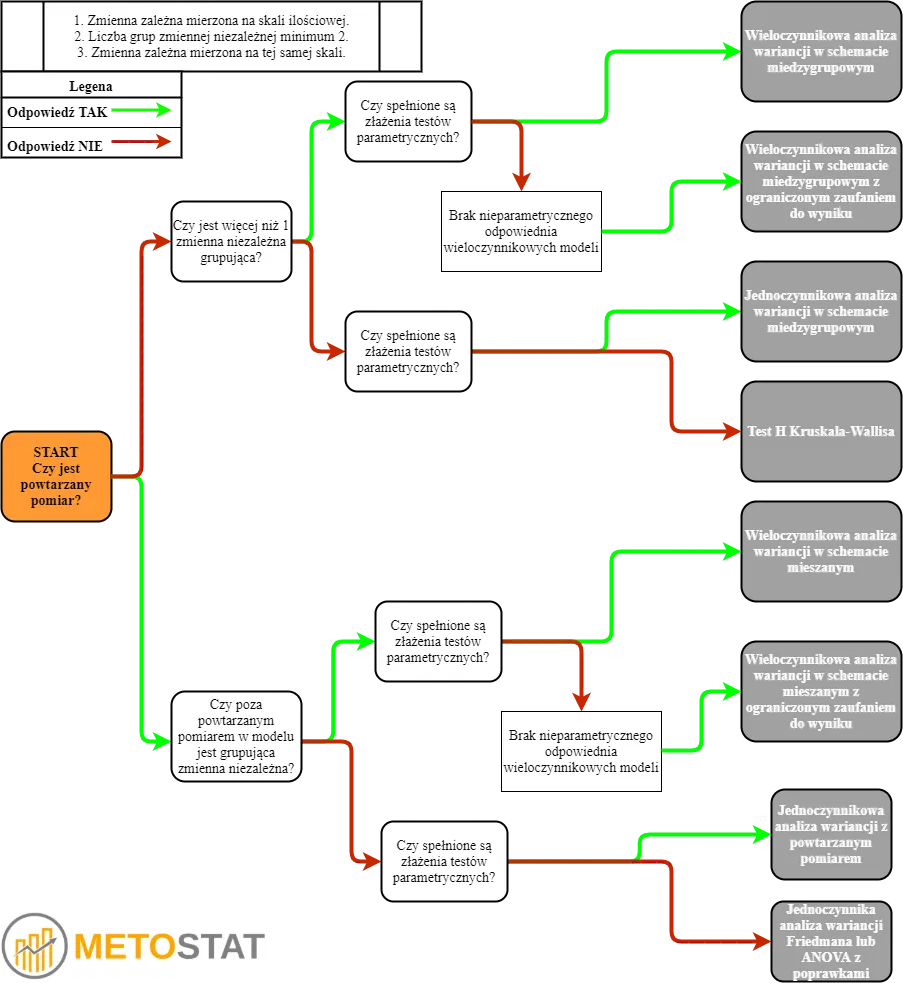

Wykorzystanie diagramów decyzyjnych w wyborze testu
Diagramy decyzyjne są niezwykle pomocnym narzędziem w procesie wyboru odpowiednich testów statystycznych. Aby stworzyć diagram, należy najpierw zidentyfikować rodzaj danych, które posiadamy, oraz cel analizy. Diagram powinien prowadzić użytkownika przez kluczowe pytania, takie jak: "Czy dane są ilościowe czy jakościowe?" oraz "Czy spełnione są założenia normalności?". Dzięki temu można w prosty sposób dotrzeć do właściwego testu, co znacznie ułatwia proces analizy.
Korzyści z użycia diagramów decyzyjnych są liczne. Po pierwsze, zapewniają one przejrzystość i usystematyzowanie procesu decyzyjnego, co jest szczególnie ważne w skomplikowanych analizach statystycznych. Po drugie, pomagają uniknąć błędów związanych z wyborem niewłaściwego testu, co może prowadzić do mylnych wniosków. Diagramy decyzyjne są także przydatne w edukacji, ułatwiając studentom zrozumienie, jakie testy należy stosować w różnych sytuacjach analitycznych.
Jak stworzyć diagram decyzyjny dla testów statystycznych?
Aby stworzyć diagram decyzyjny, należy rozpocząć od zdefiniowania kluczowych pytań dotyczących danych. Na przykład, pierwszym pytaniem może być "Czy dane są ilościowe czy jakościowe?". Następnie, w zależności od odpowiedzi, należy prowadzić użytkownika przez kolejne pytania dotyczące założeń, takich jak normalność rozkładu czy jednorodność wariancji. Diagram powinien być wizualnie czytelny, z jasno oznaczonymi ścieżkami prowadzącymi do różnych testów statystycznych, co ułatwi użytkownikowi dokonanie właściwego wyboru.Jakie korzyści płyną z użycia diagramów w analizie danych?
Użycie diagramów decyzyjnych w analizie danych przynosi wiele korzyści. Przede wszystkim, zwiększają one efektywność procesu decyzyjnego, pozwalając na szybkie zidentyfikowanie odpowiednich testów statystycznych. Ponadto, diagramy te poprawiają przejrzystość analizy, co ułatwia zrozumienie procesu zarówno analitykom, jak i osobom, które nie są ekspertami w tej dziedzinie. Dodatkowo, stosowanie diagramów może przyczynić się do lepszego zapamiętywania zasad wyboru testów, co jest szczególnie ważne w kontekście edukacji statystycznej.
Jak wykorzystać oprogramowanie do tworzenia diagramów decyzyjnych?
W dzisiejszych czasach, oprogramowanie do analizy danych oferuje zaawansowane funkcje, które mogą znacznie ułatwić tworzenie diagramów decyzyjnych. Narzędzia takie jak R, Python z biblioteką Matplotlib, czy aplikacje typu Tableau, pozwalają na wizualizację procesów decyzyjnych w sposób interaktywny i dynamiczny. Dzięki tym programom można łatwo dostosować diagramy do różnych scenariuszy analitycznych, co umożliwia szybkie wprowadzenie zmian w zależności od nowych danych lub założeń. Użytkownicy mogą również dzielić się swoimi diagramami z zespołem, co sprzyja współpracy i lepszemu zrozumieniu analizowanych danych.
Warto również zwrócić uwagę na przyszłe trendy w tej dziedzinie. Automatyzacja procesów analitycznych i wykorzystanie sztucznej inteligencji do generowania diagramów decyzyjnych mogą zrewolucjonizować sposób, w jaki podejmujemy decyzje w oparciu o dane. Systemy oparte na AI będą w stanie analizować dane w czasie rzeczywistym i sugerować odpowiednie testy statystyczne oraz wizualizacje, co pozwoli na jeszcze szybsze i bardziej trafne podejmowanie decyzji. Takie podejście nie tylko zwiększy efektywność pracy analityków, ale również pozwoli na lepsze wykorzystanie danych w różnych dziedzinach, od marketingu po badania naukowe.

